Основные положения теории вероятностей

Окружающий нас мир полон случайностей. Номера выигрышных билетов в лотерее, количество солнечных дней в году, результаты спортивных состязаний, выпадение “решки” при подбрасывании монеты, неожиданная случайная встреча, кардинально переворачивающая судьбу – все это примеры случайных событий, происходящих в повседневной жизни и влияющих на нее.

Теория вероятностей не может предсказать, произойдет или не произойдет какое_то реальное событие, а лишь предлагает математический аппарат для анализа и прогнозирования вероятности его появления. Она изучает вероятностные закономерности случайных событий, существующие объективно,

т.е. независимо от наших желаний и предпочтений.

Исторически зарождение теории вероятностей связано с поиском закономерностей в азартных играх, таких как карты и кости. Именно тогда были предприняты первые попытки математического прогнозирования и количественного определения шансов на успех. Исходными понятиями здесь являются понятия “случайное событие” и “испытание” (опыт, эксперимент).

Случайное событие – это явление, которое при одних и техже условиях может или произойти, или не произойти.

Испытание – это создание и осуществление этих неопределенных условий. Любое испытание приводит к результату или исходу, который заранее невозможно точно предсказать. Случайные события происходят повсеместно – в природе, науке, технике, экономике, военном деле и т.д. Приведем простейшие

примеры испытаний и соответствующих им случайных событий.

Важно отметить, что на самом деле “случайные события” вовсе не случайны просто для их расчета пришлось бы учесть такое количество факторов и произвести расчеты такой сложности, что никто этим не занимается. Однако с совершенстованием компьютеров и датчиков люди cмогут анализировать данные все

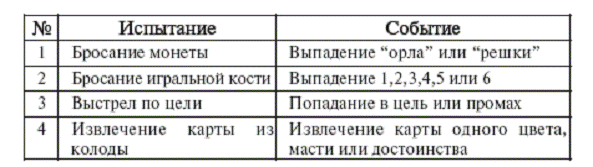
Табл 3. Примеры простейших испытаний и событий

быстрее и точнее и многие события перестают быть случайными.

Например, попадание снаряда в цель перестало быть случайным, когда в нем появился компьютер, рассчитывающий и корректирующий траекторию полета. Выигрыш в рулетку сотни лет считался случайностью, пока хитрые игроки не наловчились передавать данные об игре через видеокамеру в суперкомпьютер, который смог рассчитать, на какую цифру упадет шарик. С развитием нанотехнологии компьютеры станут еще мощнее и компактнее, а значит, многие события перестанут быть случайными и станут не только предсказуемыми, но и управляемыми.

Случайные события могут быть:

а) достоверными или невозможными;

Достоверным называется событие, которое в данных условиях всегда происходит, невозможным – если оно никогда не может быть результатом данного испытания. Например, при бросании монеты событие А – “Выпадение какой_либо стороны монеты” будет достоверным, а B – “Одновременное выпа дение “решки” и “орла”” – невозможным.

б) зависимыми или независимыми;

Если появление одного события влечет за собой появление другого, то говорят, что второе событие зависит от первого.

в) равновероятными или неравновероятными;

Например, в случае бросания игральной кости события выпадения каждой цифры равновероятны (если, конечно, это “честная” кость, без смещенного центра тяжести).

А вот вероятности события “В полдень в Москве выпадет снег” будут сильно различаться в зависимости от времени года, соответствующего данному испытанию.

К определению самого понятия вероятности существует несколько различных подходов. Мы рассмотрим лишь те из них, которые необходимы нам для понимания изучаемых квантовых явлений, а именно – классический и статистический подходы.

Вероятность – это отношение числа благоприятных событию

исходов m к общему числу всех равновозможных исходов n

Обычно вероятность обозначают буквой P (от англ. “probability” _ вероятность). Вероятность в данном случае понимается как количественная мера объективной возможности появления случайного события А и определяется формулой:

В нашем примере событиям выпадения красного, зеленого и желтого шара будут соответствовать вероятности 6/10, 3/10 и 1/10.

Функция вероятности обладает некоторыми специальными свойствами:

1. 0<P<1 , так как количество благоприятных исходов не может быть больше их общего числа.

2. Вероятность достоверного события = 1

3. Вероятность невозможного события = 0

Статистическое определение вероятности

Классическим подходом к вероятности удобно пользоваться,

когда количество всех равновозможных исходов в опыте ограничено и не

слишком велико. Однако эти условия не всегда соблюдаются на практике: иногда

приходится решать задачи, в которых число исходов постоянно меняется или бесконечно велико. Кроме того, не всегда события могут быть равновероятными.

Практика показывает, что массовые случайные явления обладают одним уникальным свойством: с увеличением числа испытаний повышается устойчивость их появления. Например,если повторить опыт бросания монетки 100 раз, то примерно в 50% испытаний выпадет “орел”, а в 50% _ “решка”. Если увеличить число испытаний до 1000 раз, это в конце концов приведет к еще большей устойчивости частоты полученных значений, а это уже определенная закономерность.

При статистическом подходе нас интересует не исход отдельно взятого испытания, а то, что получается в результате его многократного повторения, то есть в качестве статистической вероятности события принимают частоту появления того или иного события при неограниченном увеличении числа испытаний.

Например, если в результате достаточно большого числа испытаний оказалось, что относительная частота весьма близка к 0.4, то это число можно принять за статистическую вероятность события.

Статистический вероятностный подход используется повсеместно для анализа и прогнозирования событий, процессов,явлений. На его основе построены некоторые научные теории физики, квантовой механики, эволюции, генетики, информатики и др. Вероятностно_статистические методы широко при меняются в промышленности для контроля качества продукции, технической диагностики оборудования, организации массового обслуживания, астрономических наблюдений и т.д.

В рамках статистического подхода вводится понятие плотности распределения вероятности р(х), вид функции которой определяет закон распределения случайных величин. Существуют самые разные законы распределения: равномерное распределение, распределение Пуассона, распределение Бернулли и др., но наиболее распространено в природе так называемое нормальное распределение, или распределение Гаусса. На рисунке представлен вид функции такого нормального распределения, а смысл его заключается в том, что в результате большого числа испытаний относительная частота появления какого-то события группируется вокруг некоторого среднего числа, которое и можно принять за значение статистической вероятности.

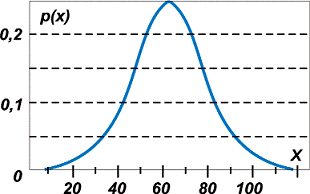
Рис 39. График функции плотности вероятности при нормальном распределении

Следующий пример наглядно иллюстрирует данный закон распределения: предположим, мы высыпаем мешок гороха на пол, держа его в одном и том же вертикальном положении. В принципе, после этого существуют некоторая вероятность обнаружить горошину в любом месте комнаты, даже в самом дальнем углу. Однако вероятность того, что мы найдем горошину в самом центре образовавшейся на полу “кучки”, гораздо выше. Значение вероятности, соответствующее координате центра кучки, мы и принимаем за статистическую вероятность.

Другой пример: пусть производится серия выстрелов по цели. Если учесть, что стрелки палят не наобум, а прилагают все усилия, чтобы попасть в “яблочко”, то вероятность попадания пули будет возрастать с приближением к центру мишени. Но “вернемся к нашим баранам”. Итак, мы решаем задачу нахождения микрочастицы в некотором объеме dV, например, ищем местоположение электрона в атоме. Как мы уже знаем, из-за несовершенства измерительных приборов мы не можем точно указать его местоположение, а можем лишь указать вероятность dP его местонахождения в той или иной части объема dV.

Кроме того, мы знаем, что эта вероятность dP прямо про порциональна dV и связана с ней следующим соотношением:

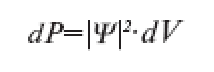
Перепишем данное уравнение в виде:

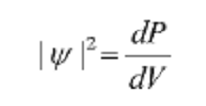
Теперь ясно видно, что |_|2 определяет вероятность нахождения частицы в некоторый момент времени t в некотором объеме dV, то есть фактически место ее нахождения в точке с координатами x,y,z (объем имеет три измерения)

В атоме водорода единственный электрон как бы образует вокруг ядра электронное облако – облако отрицательного заряда, плотность которого в некоторой точке характеризует вероятность нахождения там электрона. На рисунке показана вероятность обнаружить электрон на расстоянии r от ядра атома водорода.

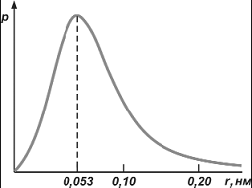
Рис 40. График вероятности обнаружения

электрона на разном расстоянии от ядра

Максимальная вероятность найти электрон соответствует расстоянию r=0,053нм. Вполне возможно, что в некоторый момент электрон находится или ближе к ядру, или дальше, но вероятность его обнаружения при этом убывает.

Область пространства, для которой вероятность обнаружения электрона составляет 95%, называется атомной орбиталью.

Итак, мы усвоили еще одну важную особенность квантовой механики:

Чтобы определить волновую функцию частицы для конкретной задачи, физики решают уравнение Шредингера, которое учитывает влияние электромагнитных сил на ее движение. Это дифференциальное уравнение в частных производных второго порядка.

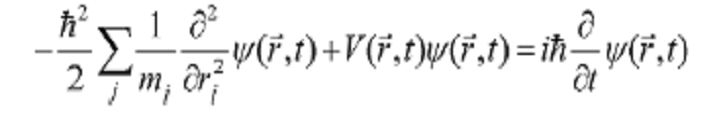
Страшно? Для решения этого уравнения потребутся знания, которые не может обеспечить школьная программа по математике, поэтому мы не будем обсуждать его в нашем курсе. Заметим лишь то, что для квантового мира уравнение Шредингера играет ту же роль, что законы Ньютона для мира классического.